Program Linear Kelas XI | Materi, Contoh Soal, dan Pembahasan

 A. Pengertian

Program linear adalah cara untuk memecahkan suatu persoalan untuk memperoleh hasil optimal $($ nilai maksimum atau minimum $)$ dari suatu model matematika yang disusun dari hubungan linear. 

Jika kita mencari pengertian di berbagai refrensi, kita akan menemukan ada banyak pengertian dari program linear. Namun, pada intinya program linear bisa kita sebut sebagai "metode optimasi", artinya bagaimana kita menentukan nilai maksimum atau nilai mininum dari suatu permasalahan.

Contoh dalam kehidupan sehari-hari, misalnya bagaimana kita menekan biaya produksi suatu pabrik atau perusahaan agar biaya yang dikeluarkan seminimal mungkin, tetapi hasil atau keuntungan yang di peroleh semaksimal mungkin.

B. Prasyarat

Sebelum mempelajari materi program linear ada materi prasyarat yang harus di pelajari antar lain,

1. Sistem persamaan linear dua variabel $($SPLDV$)$  

2. Sistem pertidaksamaan dua variabel $($SPtDV$)$ linear-linear

Contoh:

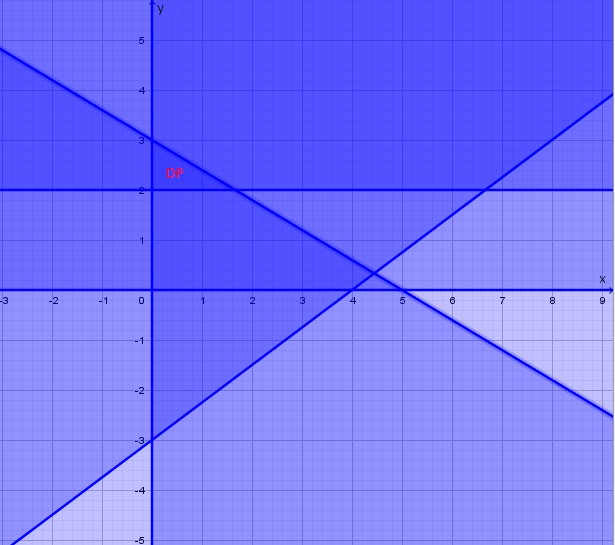
1.      Tentukan daerah himpunan penyelesaian dari pertidaksamaan linear satu variabel berikut

a. $x\geq 0$ 

b. $y\geq 0$

c. $y \geq 2$    

d. $3x-4y \leq 12$    

e. $3x+5y \leq 15$    

2.      Dari grafik pada poin a-e pada nomor 1, lukis ulang grafik tersebut dalam satu bidang kartesius, kemudian tentukan daerah penyelesaiannya 

Penyelesaian:

1.   untuk menyelesaikan masalah tersebut pertama-tama kita harus gambar grafiknya dulu kemudian kita tentukan daerah penyelesaiannya

       a. $x\geq 0$

            b. $y\geq 0$

        c. $y \geq 2$  

                d. $3x-4y \leq 12$  

                    e. $3x+5y \leq 15$   

            2.  Jika grafik a-e di gabung dalam satu bidang kartesius di peroleh grafik seperti di bawah dengan daerah penyelesaian yaitu daerah yang terkena arsiran oleh kelima daerah penyelesaian grafik tersebut.

C. Menyusun model matematika dan menyelesaikan masalah yang berkaitan dengan program linear

Dalam kehidupan sehari-hari banyak penerapan program linear, misalnya pada saat seorang penjahit ingin membuat dua jenis baju dari dua bahan kain.

Seorang penjahit memiliki 10 m kain satin dan 6 m kain renda. Dari bahan tersebut akan dibuat dua model baju. Baju I memerlukan 2 m kain satin dan 1 m kain renda, sedangkan baju II memerlukan 2 m kain satin dan 1,5 m kain renda.

a.   Dari permasalahan tersebut buatlah model matematika yang sesuai $($dalam bentuk persamaan atau pertidaksamaan$)$

b.  Jika harga jual baju I sebesar Rp400.000,00 dan baju II sebesar Rp500.000,00. Dapatkah kalian menentukan hasil penjualan maksimum yang bisa diperoleh penjahit tersebut.

Penyelesaian

a.. Untuk membuat model matematika dari permasalahan tersebut kita bisa menggunakan bantuan tabel berikut

	Banyak Baju  I  $(x)$	Banyak Baju  II  $(y)$	Total
Kain satin	2	2	10
Kain renda	1	1,5	6

    Berdasarkan tabel tersebut kita susun dalam bentuk pertidaksamaan seperti dibawah 

    1) $2x+2y \leq 10$

    2) $x+1,5y \leq 6$

kita menggunakan tanda "$\leq $" karena stok kain yang tersedia hanya 10 m dan 6 m, artinya kita tidak boleh membuat baju melebihi stok kain yang tersedia.

b. Untuk menentukan nilai optimum $($nilai maksimum/minimum$)$ dari suatu permasalahan program linear kita bisa menggunakan metode titik pojok ataupun metode garis selidik. Namun, pada pembahasan kali ini kita hanya akan membahas metode titik pojok. 

Adapun langkah-langkah menyelesaikan permasalahan program linear menggunakan metode titik pojok sebagai berikut.

a.     Buatlah model matematika dari masalah tersebut. Tentukan fungsi kendala dan fungsi tujuannya

b.  Gambarlah grafik dari sistem pertidaksamaan yang di peroleh pada poin a dan tentukan daerah penyelesaiaanya

c.       Tentukan titik pojok dari grafik tersebut

d.      Substitusi titik pojok yang di dapatkan pada poin c ke dalam fungsi tujuan

e.   Nilai terbesar merupakan nilai maksimum dan nilai terkecil adalah nilai minimum.

Lebih lengkapnya perhatikan penyelesaian berikut ini

a. Model matematika

	Banyak Baju  I  $(x)$	Banyak Baju  II  $(y)$	Total
Kain satin	2	2	10
Kain renda	1	1,5	6
Harga Jual	400.000	500.000	....

        fungsi kendala:

        1. $2x+2y \leq 10$

        2. $x+1,5y \leq 6$

        3. $x \geq 0$

        4. $y \geq 0$

        tambahan fungsi kendala pada pertidaksamaan 3 dan 4 dikarenakan banyak baju yang di hasilkan tidak mungkin bernilai negatif

fungsi tujuan/fungsi objektif $($fungsi yang akan dicari nilai maksimum/minimum$)$

$f(x,y)=400.000x+500.000y$

b. menggambar grafik dan menentukan daerah penyelesaian dari fungsi kendala

     menentukan titik potong terhadap sumbu x dan y dari fungsi kendala 1 dan 2

    1. $2x+2y \leq 10$

x	0	5
y	5	0

            koordinat titik potong terhadap sumbu x dan y yaitu $(5, 0)$ dan $(0, 5)$ 

        2. $x+1,5y \leq 6$ 

x	0	4
y	6	0

            koordinat titik potong terhadap sumbu x dan y yaitu $(4, 0)$ dan $(0, 6)$

langkah berikutnya kita gambar grafikny seperti ini 

setelah itu kita tentukan daerah penyelesaiannya dari 4 fungsi kendala $($termasuk $x \geq 0$ dan $y \geq 0$ $)$. daerah penyelesaian adalah irisan daerah penyelesaian dari 4 fungsi kendala. 

c. Menentukan titik pojok

    Titik pojok adalah titik-titik potong pada daerah penyelesaian

    Titik pojok $(0, 4)$; $(3, 2)$; $(5, 0)$ dan $(0, 0)$ 

   

     d. Substitusi titik pojok ke dalam fungsi tujuan

            $f(x, y)=400.000x+500.000y$

           1. $f(0, 4)=400.000 \times 0+500.000 \times 4=2.000.000$

           2. $f(3, 2)=400.000 \times 3+500.000 \times 2=2.200.000$

           3. $f(5, 0)=400.000 \times 5+500.000 \times 0=2.000.000$

           4. $f(0, 0)=400.000 \times 0+500.000 \times 0=0$

        Nilai maksimum terjadi pada titik pojok $(3, 2)$ yaitu 2.200.000. Jadi hasil penjualan maksimum yang bisa di peroleh penjahit tersebut yaitu Rp2.000.000,00